Grandezas - Introdução
Entendemos por grandeza tudo aquilo que pode ser medido, contado. As grandezas podem ter suas medidas aumentadas ou diminuídas.
Alguns exemplos de grandeza: o volume, a massa, a superfície, o comprimento, a capacidade, a velocidade, o tempo, o custo e a produção.
É comum ao nosso dia-a-dia situações em que relacionamos duas ou mais grandezas. Por exemplo:
Em uma corrida de "quilômetros contra o relógio", quanto maior for a velocidade, menor será o tempo gasto nessa prova. Aqui as grandezas são a velocidade e o tempo.
Num forno utilizado para a produção de ferro fundido comum, quanto maior for o tempo de uso, maior será a produção de ferro. Nesse caso, as grandezas são o tempo e a produção.
Grandezas diretamente proporcionais
Um forno tem sua produção de ferro fundido de acordo com a tabela abaixo:
| Tempo (minutos) | Produção (Kg) |
| 5 | 100 |
| 10 | 200 |
| 15 | 300 |
| 20 | 400 |
Observe que uma grandeza varia de acordo com a outra. Essas grandezas são variáveis dependentes. Observe que:
Quando duplicamos o tempo, a produção também duplica.
5 min ----> 100Kg
10 min ----> 200Kg
Quando triplicamos o tempo, a produção também triplica.
5 min ----> 100Kg
15 min ----> 300Kg
Assim:
|
Duas grandezas variáveis dependentes são diretamente proporcionais quando a razão entre os valores da 1ª grandeza é igual a razão entre os valores correspondentes da 2ª |
Verifique na tabela que a razão entre dois valores de uma grandeza é igual a razão entre os dois valores correspondentes da outra grandeza.
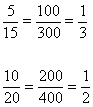
Grandezas inversamente proporcionais
Um ciclista faz um treino para a prova de "1000 metros contra o relógio", mantendo em cada volta uma velocidade constante e obtendo, assim, um tempo correspondente, conforme a tabela abaixo
| Velocidade (m/s) | Tempo (s) |
| 5 | 200 |
| 8 | 125 |
| 10 | 100 |
| 16 | 62,5 |
| 20 | 50 |
Observe que uma grandeza varia de acordo com a outra. Essas grandezas são variáveis dependentes. Observe que:
Quando duplicamos a velocidade, o tempo fica reduzido à metade.
5 m/s ----> 200s
10 m/s ----> 100s
Quando quadriplicamos a velocidade, o tempo fica reduzido à quarta parte.
5 m/s ----> 200s
20 m/s ----> 50s
Assim:
|
Duas grandezas variáveis dependentes são inversamente proporcionais quando |
Verifique na tabela que a razão entre dois valores de uma grandeza é igual ao inverso da razão entre os dois valores correspondentes da outra grandeza.


